Multiscale Gaussian Process Regression
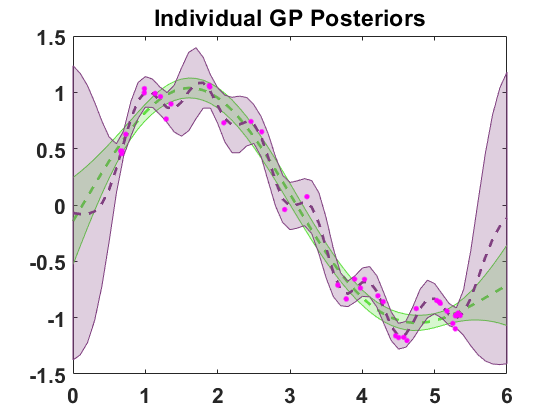 Weighted Mixture of GPs
Weighted Mixture of GPsIn this project, I focus on modeling data which exhibit multiple correlation length-scales (multiscale) using different Gaussian Process Regression (GPR) models. Such data is relevant to physical processes where a cascade of interactions happens at different scales; for example, ocean flows where micro-turbulence happens at
Inspired by the Gaussian Mixture Model (GMM) based Kalman filters, I start with a weighted mixture of GPs for the prior, and then derived a closed-form solution for the posterior weights as well as for the mean and covariance function for each mixture model, which I will refer to as the weighted mixture of GPs method. In this project, I compare the performance of some of these methods GP — ARD kernel, Gibbs kernel, additive model and weighted mixture of GPs— using synthetic 1-dimensional and 2-dimensional data. I compare computational costs, and lastly, perform regression using actual data for daily fish catch in the Lakshadweep islands of India and a sea-surface-temperature (SST) satellite measurement near the east coast of the US.