Physics-Inspired Machine Learning for PDEs
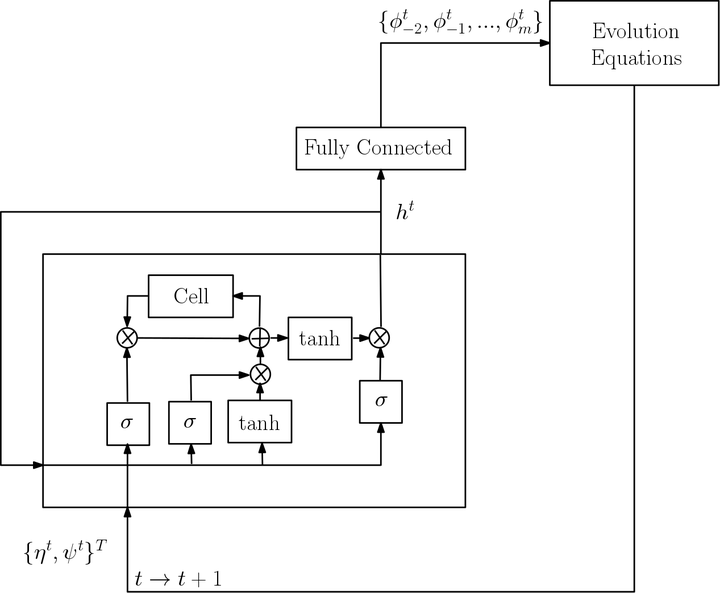 The implemented LSTM-RNN architecture coupled with the evolution equations
The implemented LSTM-RNN architecture coupled with the evolution equationsThis work studies the implementation of Machine Learning algorithms for solving nonlinear partial differential equations, in a hybrid framework. Specifically, Recurrent Neural Networks (RNN) and Convolutional Neural Networks (CNN) are used to reduce the high computational costs involved in solving such problems. We do not use Neural Nets to perform predictions for next time-steps but to replace the computationally demanding parts of the system. We implement this hybrid approach for the study of the evolution of free-surface waves. As a first test case, we study the propagation of a wave in a periodic cell. For this case we track the conservation errors regarding the time evolution of theproblem. Afterwards we model the reflection of a solitary wave on a vertical wall and compute the force acting on the wall. We also see the effect of varying hyper-parameters on the accuracy of prediction of our neuralnets, and perform leading order FLOP count compar-isons.